Matriz ortogonal — Una matriz ortogonal es un matriz cuya matriz inversa coincide con su matriz traspuesta. El conjunto de matrices ortogonales constituyen una representación lineal del grupo ortogonal . Geométricamente las matrices ortogonales representan… … Wikipedia Español
Matriz transpuesta — Saltar a navegación, búsqueda Sea A una matriz con m filas y n columnas. La matriz traspuesta, denotada con At está dada por Contenido 1 Ejemplos … Wikipedia Español
Matriz unitaria — En matemática, una matriz unitaria es una matriz compleja U, de n por n elementos, que satisface la condición: donde es la matriz identidad y es el traspuesto conjugado (también llamado el hermitiano adjunto o la hermítica) de U. Esta condición… … Wikipedia Español
Matriz de rotación — En álgebra lineal, una matriz de rotación es la matriz que representa una rotación en el espacio euclídeo. Por ejemplo, la matriz representa la rotación de θ grados del plano en sentido antihorario. En tres dimensiones, las matrices de rotación… … Wikipedia Español
Matriz simétrica — Una matriz de elementos: es simétr … Wikipedia Español
Matriz traspuesta — Sea A una matriz con m filas y n columnas. La matriz transpuesta, denotada con At está dada por En donde el elemento aji de la matriz original A se convertirá en el elemento aij de la matriz transpuesta At … Wikipedia Español
Matriz permutación — La matriz permutación es la matriz cuadrada con todos sus n×n elementos iguales a 0, excepto uno cualquiera por cada fila y columna, el cual debe ser igual a 1. De acuerdo a esta definición existen n! matrices de permutación distintas, de las… … Wikipedia Español
Matriz diagonalizable — En álgebra lineal una matriz cuadrada A se dice que es diagonalizable si es semejante a una matriz diagonal, es decir, si mediante un cambio de base puede reducirse a una forma diagonal. En este caso, la matriz podrá descomponerse de la forma A … Wikipedia Español
Grupo ortogonal — En matemática, el grupo ortogonal de grado n sobre un cuerpo F (escrito como O(n, F)) es el grupo de matrices ortogonales n por n con las entradas en F, con la operación de grupo dada por la multiplicación de matrices. Éste es un subgrupo del… … Wikipedia Español
Grupo ortogonal — En matemáticas, el grupo ortogonal de grado n sobre un cuerpo F (escrito como O(n, F)) es el grupo de matrices ortogonales n por n con las entrad … Enciclopedia Universal
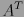 y matriz inversa
y matriz inversa 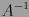 es ortogonal, siempre que
es ortogonal, siempre que 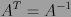 .
Por ejemplo, si B es ortogonal, entonces:
.
Por ejemplo, si B es ortogonal, entonces:
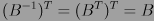 Si la matriz A y B son ortogonales entonces la matriz producto de A por B es ortogonal. Toda matriz permutación es ortogonal y también, toda matriz transformación de un sistema de coordenadas asociado a un espacio euclídeo.
Si la matriz A y B son ortogonales entonces la matriz producto de A por B es ortogonal. Toda matriz permutación es ortogonal y también, toda matriz transformación de un sistema de coordenadas asociado a un espacio euclídeo.